The answer is Timsort.
Definition
•A hybrid stable sorting algorithm, derived from merge sort and insertion sort.
•Designed to perform well on many kinds of real-world data.
•It was implemented by Tim Peters in 2002 for use in the Python programming language.
•The algorithm finds subsequences of the data that are already ordered, and uses that knowledge to sort the remainder more efficiently.
•This is done by merging an identified subsequence, called a run, with existing runs until certain criteria are fulfilled.
•It has been Python's standard sorting algorithm since version 2.3.
•It is also used to sort arrays of non-primitive type in Java SE7, on the Android platform, in GNU Octave, and Google Chrome.
Time complexity
Worst-case performance |
|
Best-case performance |
|
Average performance |
|
Worst-case space complexity |
|
Compare with other algorithms
∙Quick sort가 좋은 성능을 보이지 못하는 real world data에서 좋은 성능을 보임. 최악의 경우에도 O(nlogn)으로 안정적인 정렬 알고리즘임.
∙Merge sort, 미리 어느정도 정렬이 끝난 run으로 분할하고 병합함.
Minrun
∙run의 크기를 동적으로 구함. 이미 정렬된 subsequence를 기준으로 생성하며 만약 minrun보다 작으면 insertion sort를 사용해 subsequence를 정렬.
∙minimum run size (minrun) 를 구하는 것은 data size에 의해 결정되며 elements가 64보다 작으면 minrun은 64가 되며 이처럼 사이즈가 작은 subsequence의 경우에는 insertion sort를 수행함. (insertion sort가 32~64 범위에서 가장 빠르기 때문.)
∙size가 큰 array에서는 32~64 범위의 minrun을 가지고 array를 분할시킴.
∙크기가 64보다 작아질 때까지 수행.
Merge
∙Timsort는 run을 구하고 모든 run이 만들어졌다면 병합을 함.
∙병합은 2개씩 이루어지며 stack을 이용해 run을 push하고 앞서 push 되어있던 run과 병합을 함. (stability를 만족시키기 위해서 인접한 run끼리만 병합.)
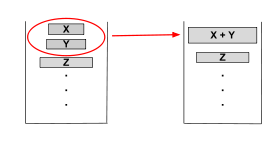
병합은 다음과 같은 조건을 만족해야만 수행함.
i) X > Y + Z
ii) Y > Z[6]
만약 X< Y+Z이면 Y는 X와Z 중 작은 것과 merge를 수행하게 됨.
Merge Memory
∙Merge sort가 그렇듯 Tim sort도 임시 메모리가 필요함.
∙두개의 run 중 작은 사이즈를 할당함.
1. 작은 사이즈의 run을 임시 메모리로 복사.
2. 복사된 run과 복사되지 않은 더 큰 사이즈의 run과 병합. (병합은 임시 메모리에 복사한 run의 메모리 시작부분부터 하나씩 저장됨.)
3. 이 때, binary search를 이용하여 순차적으로 저장하게 됨.
Galloping mode
∙대부분의 병합은 'one pair at a time' mode.
∙보통 병합은 두 run의 요소를 비교하며 병합해나가지만, 하나의 run에서 연속해서 많이 (MIN_GALLOP) pop 되면 Galloping mode를 호출하게 됨.
∙한 쪽의 맨 앞의 요소보다도 작은 요소가 다른 쪽의 요소에도 있는지 index를 2n씩 늘리며 검색.
Tim sort 알고리즘을 찾아보게 된 계기는 다음과 같다. Median of Two Sorted Arrays 문제를 푸는데 두 개의 배열을 합쳐 sort() 함수로 정렬하고 median을 구하는데 걸린 시간과 recursive로 파티션을 나눠서 median을 찾는데 걸린 시간이 비슷해서 의문을 가졌다. python에 내장되어 있는 sort() 메소드는 어떤 방식으로 작동하길래 이렇게 빠른건가. 구글링 해본 결과 python에 내장된 sort() 메소드는 Tim sort라는 알고리즘을 사용하고 있었고 이미 정렬된 배열에 대해서 매우 좋은 성능을 보이는 것을 확인할 수 있었다.
References :
About pythons built in sort method
https://stackoverflow.com/questions/1517347/about-pythons-built-in-sort-method
Python sorted 알고리즘 Timsort
https://medium.com/@fiv3star/python-sorted-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-timsort-dca0ec7a08be
timsort
http://orchistro.tistory.com/175
[번역] About Tim Sort
http://jeen.github.io/2012/01/03/about-tim-sort/
위키피디아 Timsort
'0 > algorithm' 카테고리의 다른 글
| Longest Palindromic Substring (in Python) (0) | 2019.01.19 |
|---|---|
| Median of Two Sorted Arrays (in Python) (0) | 2019.01.19 |
| Longest Substring Without Repeating Characters (in Python) (0) | 2019.01.18 |
| Add two numbers (in Python) (0) | 2019.01.18 |
| Two Sum (in Python) (0) | 2019.01.18 |


