Problem
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Note: Given n will be a positive integer.
Example 1:
Input: 2 Output: 2 Explanation: There are two ways to climb to the top. 1. 1 step + 1 step 2. 2 steps
Example 2:
Input: 3 Output: 3 Explanation: There are three ways to climb to the top. 1. 1 step + 1 step + 1 step 2. 1 step + 2 steps 3. 2 steps + 1 step
Solution
Approach 1 : Brute Force
climbStairs(i, n) = climbStairs(i+1, n) + climbStairs(i+2, n)
이렇게 풀면 시간이 정말 오래걸리겠죠 ^^!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | class Solution: def climbStairs(self, n): """ :type n: int :rtype: int """ def backtrack(i, n) : if i > n : return 0 if i == n : return 1 return backtrack(i+1, n) + backtrack(i+2, n) return backtrack(0, n) | cs |
Complexity Analysis
•Time complexity : O(2^n). Size of recursion tree will be 2^n.
Recursion tree for n=5 would be like this:
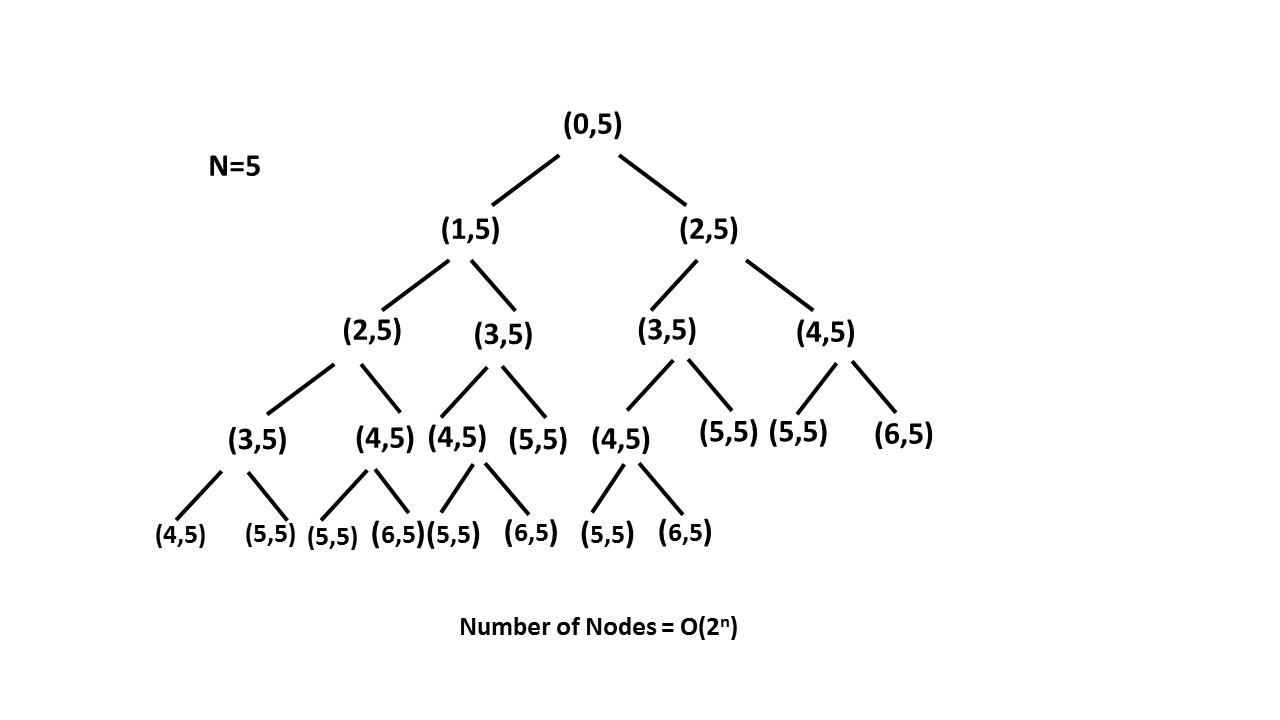
•Space complexity : O(n). The depth of the recursion tree can go upto n.
Approach 2 : Recursion with memoization
이전 방법에서는 모든 경우를 직접 계산했습니다. 하지만 계산한 값을 미리 저장(메모)해두면 정말 많은 시간을 줄일 수 있겠죠?!!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | class Solution: def climbStairs(self, n): """ :type n: int :rtype: int """ if n == 0 : return 0 res = [0]*(n+1) def backtrack(i, n) : if i > n : return 0 if i == n : return 1 # 메모이제이션 if res[i] > 0 : return res[i] res[i] = backtrack(i+1, n) + backtrack(i+2, n) return res[i] return backtrack(0, n) | cs |
Complexity Analysis
•Time complexity : O(n). Size of recursion tree can go upto n.
•Space complexity : O(n). The depth of recursion tree can go upto n.
Source
'0 > algorithm' 카테고리의 다른 글
| Sort linked list (in Python) (0) | 2019.01.27 |
|---|---|
| Minimum Increment to Make Array Unique (in Python) (0) | 2019.01.25 |
| Add Binary (in Python) (0) | 2019.01.23 |
| Rotate Image (in Python) (0) | 2019.01.23 |
| Permutations (in Python) (0) | 2019.01.23 |